Multiple Destination Tours' and Paths' Efficient Determination in Directed Graphs
$ 38.5
Description
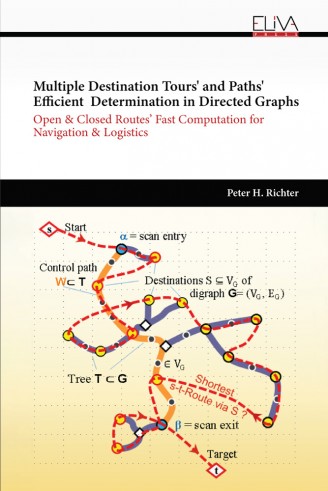
The described heuristic A efficiently computes open and closed near-optimal routes in digraphs G to meet all destinations S in V(G). A does not require graphs observing the triangle inequality, determines open or closed tours by one algorithm, and draws advantage from using planar graphs. A relies on the meta-heuristics
- Advanced Scan of Spanning Trees ASS applied to approx. Steiner trees T in G spanning S,
- Tree Structure Adaption TSA that overcomes “flaws” of tree T hampering good results,
- Confined Complete Enumeration CCE as an essential local optimization feature, and
- Compact Priority Queue CPQ Θ considerably reducing run-time.
Algorithm A doesn't surpass standard deviations q-max= 1,86 %, referring to the optima for S < 16, and it remains real-time capable (≤ 2 sec) for S < 150. Regarding larger problem sizes 100 < S < 1.000, the use of CCE with TSA gets 15% length improvement compared to the pure use of ASST. This holds also for S= 1.000 if the denseness S / V(G) is not too high. Testing real-time ability (nominal 2 sec) algorithm A running on a 2,70 GHz PC using graphs with Θ=3 computes tours with TSA: S= 115 and without TSA: S= 1590. That means that time-critical apps processing higher problem sizes should use CCE without TSA to keep real-time ability provided a loss of about 5% solution quality is accepted. Since A tackles the cases S= V(G) and S< V(G), s= t and s not t, digraphs and undirected graphs, it efficiently solves the Symmetric and Asym. Traveling Salesman Walk Problem, the Symmetric and Asym. Steiner Traveling Problem, and the Symmetric and Asym. Steiner Traveling
